- This topic has 4 replies, 3 voices, and was last updated 3 years, 8 months ago by
.
-
Posts
-
-
Hello, I’m trying to learn some music theory and I started with 12 tone equal temperament (12-TET) and it’s approximation of pure intervals. I created some code that generates 12 equally spaced intervals just like how 12-TET says to do. I then plotted some of the common ratio’s from the fundamental to try and see which of the ratio’s line up with the 12-TET approximation (to see how good it is!). The gif (
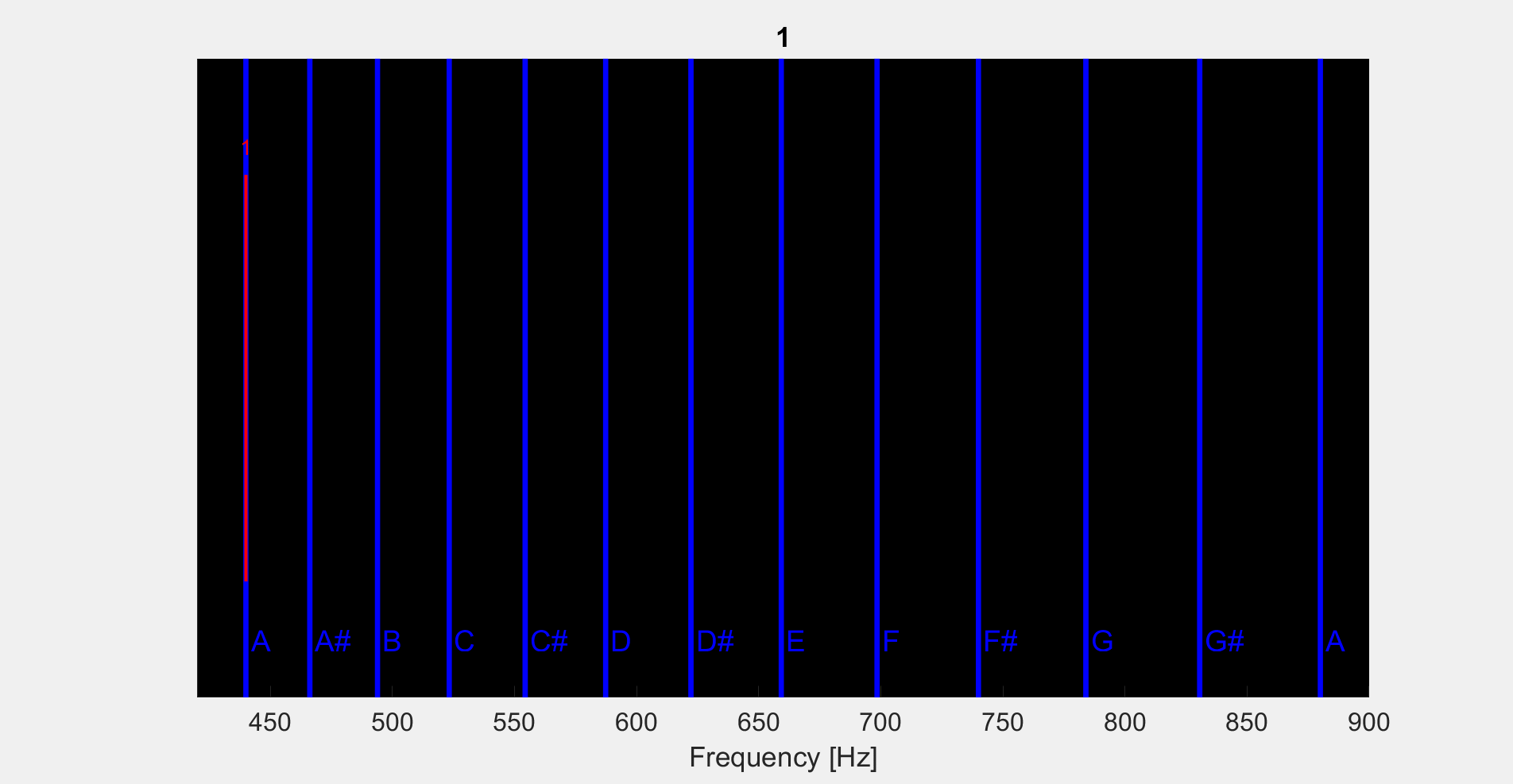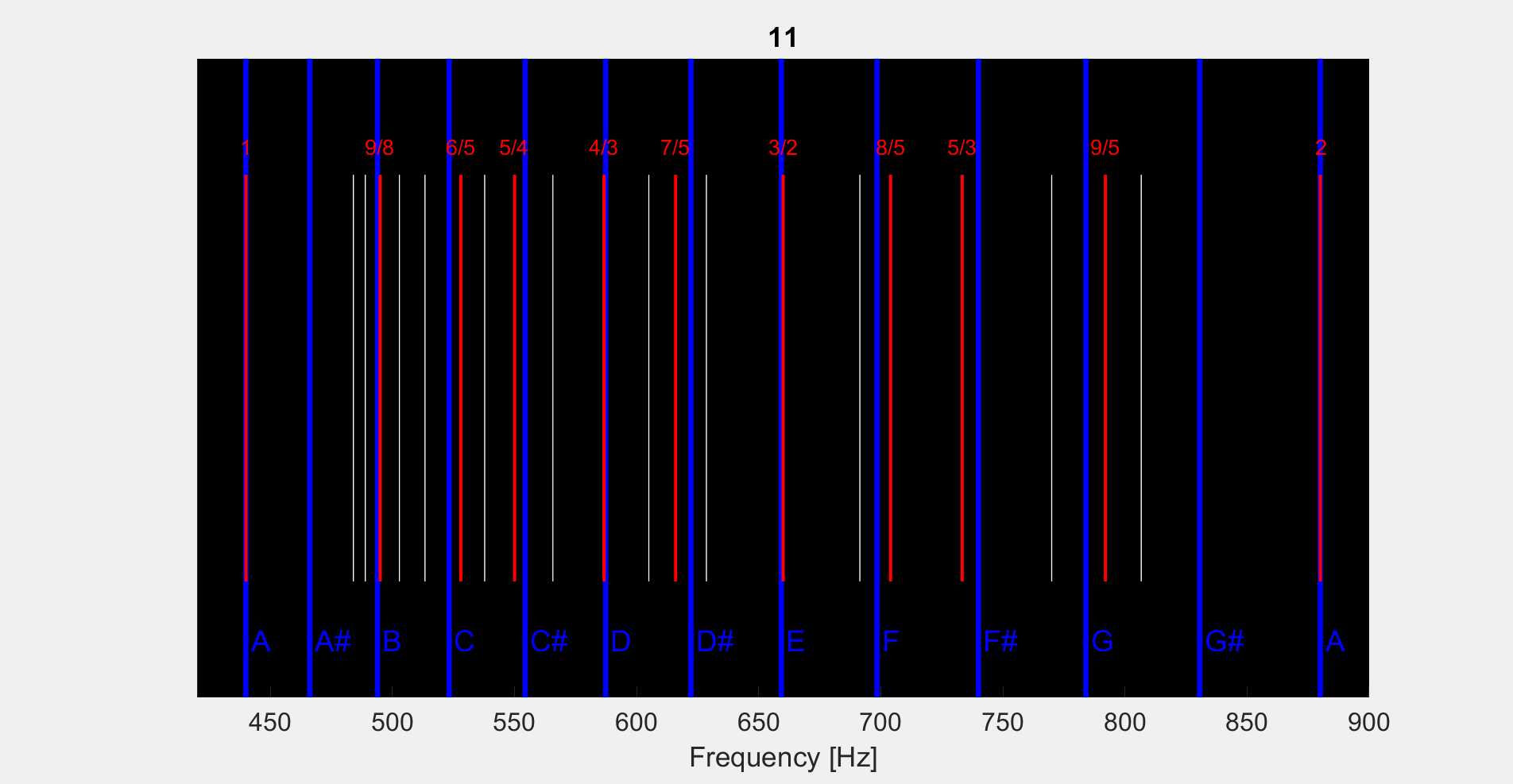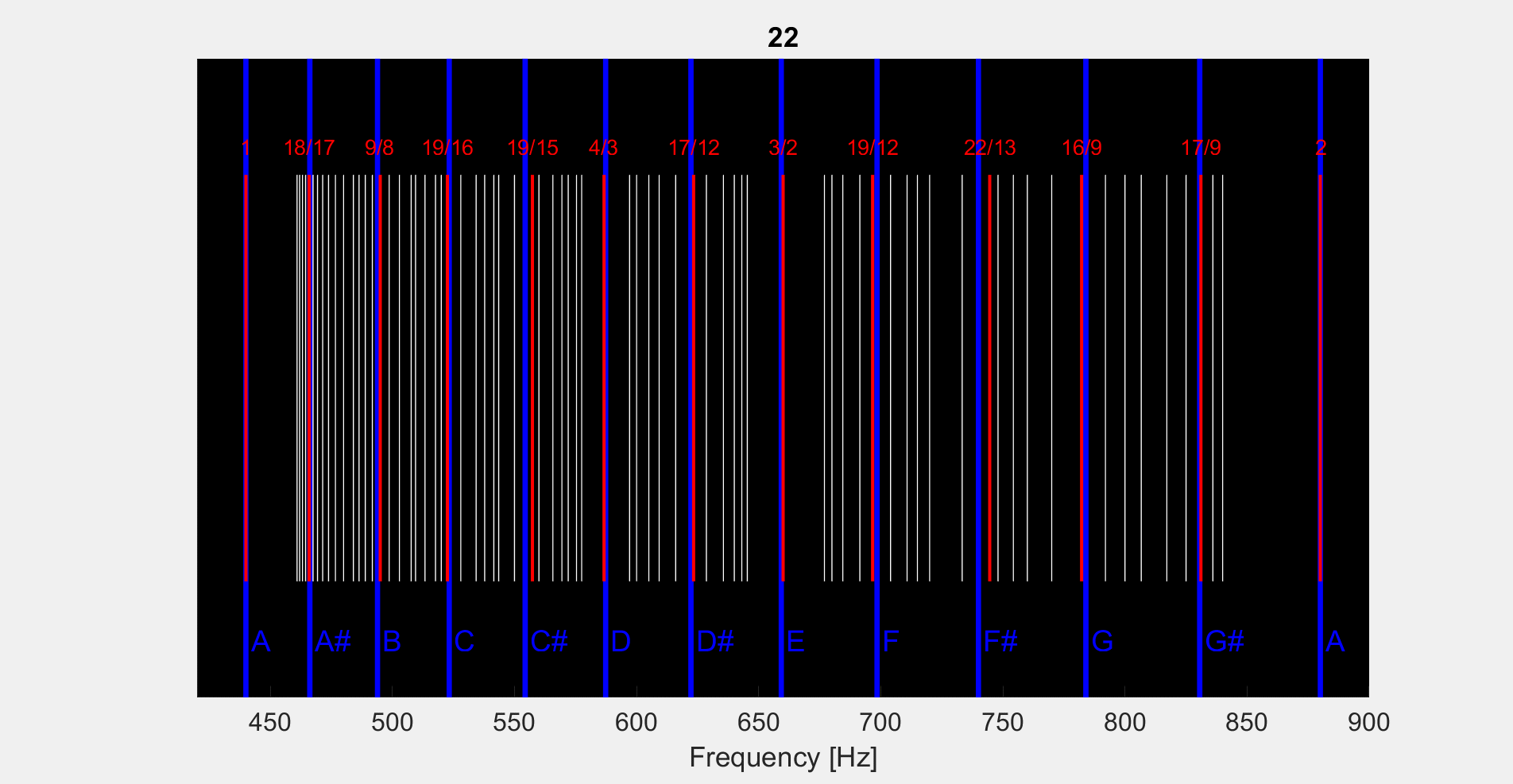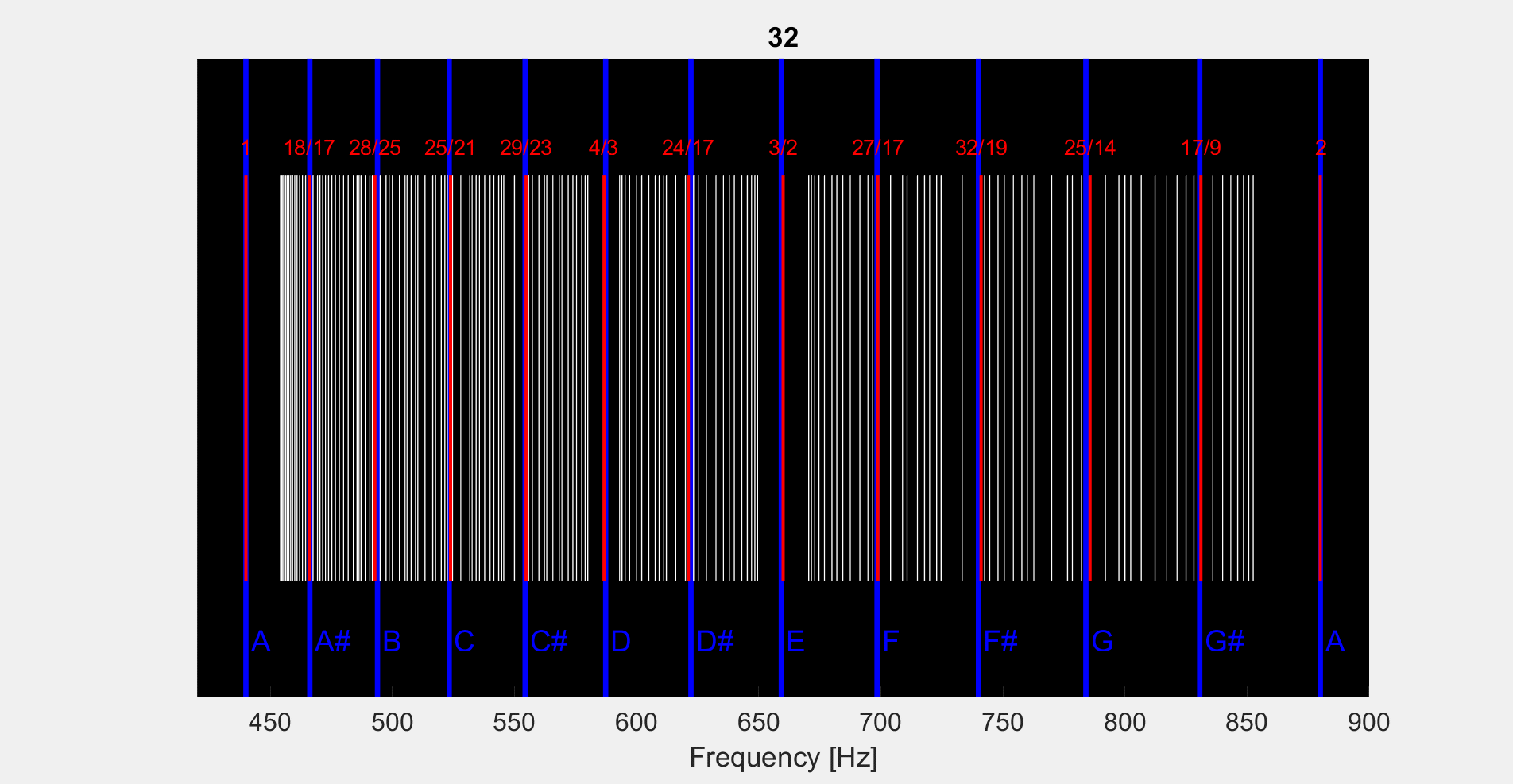) is attached: the red lines are the ratio’s that are closest to one of the 12 notes. White lines are other ratios that aren’t that close to the 12 notes. I scan as a function of “complexity” of the ratios, meaning I slowly increase the size of the integers allowable in the numerator and denominator of the ratio. I hope the gif will sorta speak for itself.You can see that as we scan the “complexity” of the ratios, we get closer and closer to the “true” interval that 12-TET is approximating. Obviously, we only care about “simple” ratios, so this needs to be truncated if this is to mean anything. But here lies my question to you all: according to this (https://en.wikipedia.org/wiki/Equal_temperament) Wikipedia article (and other sources) I found, the simple ratio’s that 12-TET is approximating are:
1, 16/15, 9/8, 6/5, 5/4, 4/3, 64/45, 3/2, 8/5, 5/3, 16/9, 15/8, 2My confusion is why are these the ratio’s that they claim 12-TET approximates? For example, why claim that the tritone in 12-TET is approximating the ratio 64/45 when the ratio 24/17 is both closer to the tritone AND a smaller (simpler) ratio? Another example: why say that we are approximating the ratio 16/15 in the minor second of 12-TET when 17/16 is even closer and 18/17 is even closer! If your answer is “well 16/15 is a simpler ratio and we are seeking to approximate simple intervals”, then why not 10/9 or 11/10 or 12/11 or 13/12 and so on? Those are also simpler and relatively close!
Overall I would just like to know how they chose which intervals they claim that we are approximating with this system, because according to what I’ve been playing with, the simplest intervals we are approximating are:
1, 11/10, 9/8, 6/5, 5/4, 4/3, 7/5, 3/2, 8/5, 5/3, 9/5, 11/6, 2
Instead of:
1, 16/15, 9/8, 6/5, 5/4, 4/3, 64/45, 3/2, 8/5, 5/3, 16/9, 15/8, 2 -
Hi Jacob,
I can’t say you started your study of music theory with the most practical aspect of it 😉
But I’ll try to give you at least a partial response.To begin with, I don’t think that the pitches obtained in the equal temperament are trying to “approximate” anything. They are what they are; it turns out that those pitches are reasonably usable. “Reasonably usable” should be interpreted to mean:
– they are close enough to the “pure” and “small” ratios of just intonation to preserve consonance (more on this below).
– they guarantee that transposition will be possible in all twelve keys
But one should always keep in mind that there is a lot of cultural subjectivity in this.The Wikipedia article you cite only compares the equal temperament with one particular set of just intonation ratios.
The problem with just intonation is that there is no one single just intonation and therefore not a single series of “simple ratios”. In fact, there is an infinity of “justly tempered” 12-tone scales starting from a given reference pitch (frequency).
Very often, products of integer powers of 3 and 5 are used, together with powers of 2. This is called “5-limit just intonation”. Powers of 5 produce thirds; powers of 3 produce fifths; powers of 2 map the result back between the boundaries of the octave.
For example, assuming we start from a pitch we call A, we can define the pitch for C# in at least two different ways:
– using thirds you can go “up” one factor 5 and “down” two factors 2: 5.2^(-2) resulting in a ratio 5/4
– using fifths you can go up four factors 3 and down six factors 2: (3^4)(2^-6) resulting in a ratio 81/64
The results will be extremely close. If A = 440 Hz, C# will be 550 Hz in the first case and 556 Hz in the second case.If you want all the glory details about just intonation and how to produce a 12-tone scale using the 5-limot tuning, see this Wikipedia article… heavy stuff!
Hope this helps.
-
Thank you for your reply!
So since the particular set of just intonation ratios is arbitrary, do you have a guess as to why the authors of this Wiki page chose this set in particular? Based on their choices, it seems like there must be some historical/structural reasoning to this, given how the ratios could be ‘closer’ and ‘smaller’. Is there any underlying structure/reason as to why one would choose some ratios over others?
It does seem like they’re doing something similar to your 5-limit just intonation idea. All of those ratios have only 2,3, and 5 in their prime decomposition. So is that the reason they chose those ratios? To avoid any primes over 5? I asked a friend and that was his hypothesis. He said that musical ratios tend to stick to prime decompositions with primes 2,3, and 5.
-
Yes, 5-limit tuning is apparently a very common technique, but not the only one.
If you want to build a major scale in just intonation, you usually specify some constraints; for example, you want “pure” a third and fifth, and “pure” IV and V chords. That will produce a set of ratios that satisfy your constraints, at the expense of other intervals and chords that will consequently be less “pure”. Itis always a compromise.
I don’t know why the authors of that Wikipedia article picked those specific ratios and to be honest, I don’t really care… I suppose they result from some constraints as mentioned above, but I have no idea which ones and I am not going to investigate! I understand the general principles of tunings, but I am perfectly happy to ignore the nitty gritty details!
-
-
-
-
- You must be logged in to reply to this topic.
